সংজ্ঞা:
পরিঘাত ডেটাসেটের বণ্টন কতটা চ্যাপ্টা (Flat) বা সূঁচালো (Peaked) তা বোঝায়। এটি ডেটার বণ্টন আকৃতির বৈশিষ্ট্য নির্দেশ করে।
প্রকারভেদ:
১. লেপ্টোকুরটিক (Leptokurtic): বণ্টন খুব সূঁচালো। কেন্দ্রীয় অংশে বেশি মান ঘন।
২. মেসোকুরটিক (Mesokurtic): স্বাভাবিক বণ্টন; গড়পড়তা মান ঘন।
৩. প্ল্যাটিকুরটিক (Platykurtic): বণ্টন অপেক্ষাকৃত চ্যাপ্টা; কেন্দ্রীয় অংশে কম মান ঘন।
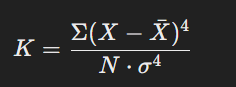
পরিঘাত নির্ণয়ের সূত্র:
বঙ্কিমতা (Skewness)
সংজ্ঞা:
বঙ্কিমতা ডেটাসেটের বণ্টন কেন্দ্রীয় বিন্দু থেকে ডানদিকে বা বামদিকে কতটা ঝোঁক প্রমাণ করে।
প্রকারভেদ:
১. ধনাত্মক বঙ্কিমতা: লেজ ডানদিকে দীর্ঘ; গড় > মধ্যক > বহুলক।
২. ঋণাত্মক বঙ্কিমতা: লেজ বামদিকে দীর্ঘ; গড় < মধ্যক < বহুলক।
৩. শূন্য বঙ্কিমতা: বণ্টন সমান; গড় = মধ্যক = বহুলক।
বঙ্কিমতা নির্ণয়ের সূত্র:
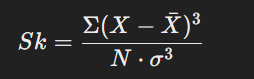
সংজ্ঞা:
সূঁচালতা ডেটাসেটের বণ্টনের কেন্দ্রীয় অংশের চারপাশে ওঠানামার মাত্রা নির্দেশ করে। এটি পরিঘাতের সাথে সম্পর্কিত এবং ডেটাসেটের তীক্ষ্ণতা নির্ধারণে ব্যবহৃত হয়।
2, 1, 0, 5, 6, 7,-4
একটি বিন্যাসের গড় 25, মধ্যমা 20 ও বিভেদাঙ্ক 50%।
পরিঘাত (Impact)
পরিঘাত বলতে বোঝানো হয় কোনো ঘটনার প্রভাব বা ফলাফল, যা নির্দিষ্ট একটি পরিস্থিতি বা ব্যবস্থার উপর পড়ে। এটি একটি ঘটনা বা কার্যক্রমের কারণে হওয়া পরিবর্তন বা প্রতিক্রিয়া হিসেবে দেখা যায়। পরিঘাত বিভিন্ন প্রেক্ষাপটে ব্যবহৃত হয়, যেমন বিজ্ঞান, সমাজবিজ্ঞান, প্রকৌশল, পরিবেশ বিজ্ঞান এবং ব্যবসা ক্ষেত্রে।
পরিঘাতকে বিভিন্নভাবে শ্রেণীবদ্ধ করা যায়, যা নির্ভর করে তার প্রকৃতি, উৎস এবং প্রভাবের মাত্রার উপর। প্রধান শ্রেণী বিভাগগুলো হলো:
পরিঘাত একটি বহুমাত্রিক ধারণা, যা নির্দিষ্ট কোনো ঘটনা বা কার্যক্রমের ফলাফল হিসেবে ঘটে। এটি ইতিবাচক বা নেতিবাচক হতে পারে এবং সময়, স্থান, প্রভাবের মাত্রা ও প্রাকৃতিক-মানবসৃষ্ট উৎসের ভিত্তিতে শ্রেণীবদ্ধ করা যায়। পরিঘাতের সঠিক বিশ্লেষণ প্রয়োজনীয় পদক্ষেপ নিতে এবং প্রভাব কমানোর জন্য গুরুত্বপূর্ণ।
প্রথম চারটি কাঁচা পরিঘাতকে (Raw Moments) কেন্দ্রীয় পরিঘাতের (Central Moments) মাধ্যমে প্রকাশ করতে হলে, আমরা কাঁচা পরিঘাত এবং কেন্দ্রীয় পরিঘাতের মধ্যে সম্পর্ক ব্যবহার করি।
কাঁচা পরিঘাত এবং কেন্দ্রীয় পরিঘাতের সম্পর্ক হলো:
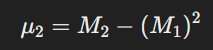
কারণ কেন্দ্রীয় পরিঘাতের প্রথম পরিঘাত সবসময় শূন্য হয়।
![]()
এখানে:

![]()
এখানে:
![]()
![]()
এখানে:
![]()
পরিঘাত (Kurtosis) হলো ডেটাসেটের বণ্টন কতটা সূঁচালো বা চ্যাপ্টা তা বোঝানোর পরিসংখ্যানিক মাপকাঠি। এটি ডেটার কেন্দ্রীয় বণ্টনের বৈশিষ্ট্য বুঝতে এবং বিভিন্ন পরিস্থিতিতে ব্যবহার করতে গুরুত্বপূর্ণ। নিচে এর প্রয়োজনীয়তা ও ব্যবহার আলোচনা করা হলো:
১. ডেটাসেটের বণ্টনের বৈশিষ্ট্য নির্ধারণ:
পরিঘাতের মাধ্যমে ডেটাসেটের কেন্দ্রীয় মানের চারপাশে বণ্টনের প্রকৃতি (তীক্ষ্ণতা বা চ্যাপ্টা) নির্ধারণ করা যায়।
২. বহিরাগত মান (Outliers) শনাক্ত করা:
ডেটাসেটে বহিরাগত মানের উপস্থিতি পরিঘাতের মানের মাধ্যমে বোঝা যায়। লেপ্টোকুরটিক বণ্টন বহিরাগত মানের উপস্থিতি নির্দেশ করে।
৩. ঝুঁকি বিশ্লেষণ:
পরিঘাত ব্যবহার করে ঝুঁকি বিশ্লেষণ করা যায়। ফিনান্স এবং বিনিয়োগ ব্যবস্থাপনায় এটি ব্যবহার করে উচ্চ ঝুঁকির সম্পদ শনাক্ত করা হয়।
৪. গুণমান নিয়ন্ত্রণ (Quality Control):
গুণমান নিয়ন্ত্রণের ক্ষেত্রে উৎপাদিত পণ্যের বৈচিত্র্য এবং মানের তীক্ষ্ণতা বিশ্লেষণে পরিঘাত ব্যবহার করা হয়।
৫. সিদ্ধান্ত গ্রহণে সহায়ক:
ডেটাসেটের বণ্টনের ধরন বোঝার মাধ্যমে বিভিন্ন ক্ষেত্রে সঠিক সিদ্ধান্ত গ্রহণে সহায়তা করে।
১. পরিসংখ্যানিক বিশ্লেষণে:
পরিঘাতের মাধ্যমে ডেটাসেটের কেন্দ্রীয় বণ্টনের গঠন বিশ্লেষণ করা হয়। এটি গবেষণার জন্য বণ্টনের ধরণ সম্পর্কে ধারণা প্রদান করে।
২. অর্থনীতি ও ফিনান্সে:
ফিনান্স সেক্টরে পরিঘাত ব্যবহার করে উচ্চ ঝুঁকির সম্পদ বা স্টক শনাক্ত করা হয়। লেপ্টোকুরটিক বণ্টন উচ্চ ঝুঁকির ইঙ্গিত দেয়, আর প্ল্যাটিকুরটিক বণ্টন কম ঝুঁকির।
৩. প্রকৌশল ও মান নিয়ন্ত্রণে:
প্রকৌশলে উৎপাদিত পণ্যের বৈচিত্র্য নির্ধারণে এবং মানের স্থায়িত্ব বিশ্লেষণে এটি ব্যবহৃত হয়।
৪. স্বাস্থ্য ও জীববিজ্ঞানে:
রোগের বণ্টন বিশ্লেষণ, স্বাস্থ্য গবেষণায় ডেটার বৈচিত্র্য এবং অস্বাভাবিক মান সনাক্ত করতে এটি ব্যবহৃত হয়।
৫. ঝুঁকি ব্যবস্থাপনায়:
ব্যাংকিং এবং ইনস্যুরেন্স খাতে পরিঘাত ঝুঁকি ব্যবস্থাপনার একটি গুরুত্বপূর্ণ উপাদান।
৬. গবেষণামূলক কাজে:
পরিঘাতের মাধ্যমে বিভিন্ন গবেষণার তথ্য বিশ্লেষণ এবং সঠিক ফলাফল উপস্থাপন করা যায়।
পরিঘাত ডেটাসেটের বণ্টনের প্রকৃতি এবং ঝুঁকি বিশ্লেষণের একটি কার্যকর মাপকাঠি। এটি বহিরাগত মান শনাক্তকরণ, গুণমান নিয়ন্ত্রণ, এবং ঝুঁকি ব্যবস্থাপনার জন্য গুরুত্বপূর্ণ ভূমিকা পালন করে।
বঙ্কিমতা (Curvature)
বঙ্কিমতা বলতে কোনো বস্তু, রেখা বা পৃষ্ঠের বাঁক বা বক্রতার পরিমাণ বোঝানো হয়। এটি মূলত জ্যামিতিক ধারণা, যা বস্তু বা পৃষ্ঠের আকৃতির বক্রতার মাত্রা পরিমাপ করতে ব্যবহৃত হয়। বঙ্কিমতা নির্ধারণ করা হয় নির্দিষ্ট বিন্দুতে একটি রেখার ত্রিজ্যু বা বক্রতা এবং তার সংশ্লিষ্ট গাণিতিক সম্পর্কের মাধ্যমে।
বঙ্কিমতাকে বিভিন্ন দিক থেকে শ্রেণীবদ্ধ করা যায়, যা নির্ভর করে এর প্রয়োগ এবং প্রকৃতির উপর। নিচে বঙ্কিমতার প্রধান প্রকারভেদগুলো আলোচনা করা হলো:
রেখার বঙ্কিমতা নির্ধারণ করে একটি নির্দিষ্ট বিন্দুতে রেখার কতটুকু বাঁক বা বক্রতা রয়েছে।
পৃষ্ঠের বঙ্কিমতা বোঝায় একটি পৃষ্ঠের বিভিন্ন বিন্দুতে তার বাঁক বা বক্রতার মাত্রা।
পৃষ্ঠের বা রেখার আকার তার অভ্যন্তরীণ জ্যামিতি থেকে নির্ধারিত হয় এবং এটি বাহ্যিক কোনো প্রভাবের উপর নির্ভর করে না।
এটি পৃষ্ঠের আকৃতির উপর নির্ভর করে, যা তার চারপাশের স্থানিক বিন্যাস থেকে নির্ধারিত হয়।
বঙ্কিমতা একটি গুরুত্বপূর্ণ জ্যামিতিক ধারণা, যা কোনো রেখা বা পৃষ্ঠের বক্রতার মাত্রা এবং প্রকৃতি নির্ধারণ করে। এটি বিভিন্ন প্রকারে শ্রেণীবদ্ধ করা যায়, যেমন রেখার বঙ্কিমতা, পৃষ্ঠের বঙ্কিমতা, ধনাত্মক ও ঋণাত্মক বঙ্কিমতা। বঙ্কিমতা সম্পর্কে জ্ঞান পদার্থবিজ্ঞান, প্রকৌশল, এবং গণিতের বিভিন্ন ক্ষেত্রে গুরুত্বপূর্ণ ভূমিকা পালন করে।
সূচালতা একটি পরিমাপ যা একটি ডেটা সেটের বন্টনের আকার এবং তার গড়ের সাথে সংশ্লিষ্ট অবস্থানকে বর্ণনা করে। এটি বিশেষভাবে দেখায় যে ডেটা সেটটি গড়ের চারপাশে কতটা সমমিত বা অসমমিত। সূচালতা বন্টনের আকৃতি সম্পর্কে গুরুত্বপূর্ণ ধারণা প্রদান করে।
সূচালতাকে প্রধানত তিনটি প্রকারে ভাগ করা যায়:
সূচালতা সাধারণত এই সূত্র দিয়ে গণনা করা হয়:

সূচালতা ডেটার বন্টনের আকৃতি ও তার গড়ের সাথে সম্পর্কিত অবস্থান সম্পর্কে ধারণা দেয়। এটি তিন ধরনের হতে পারে: ধনাত্মক, ঋণাত্মক এবং শূন্য। সূচালতা ডেটা বিশ্লেষণের একটি গুরুত্বপূর্ণ পরিমাপ, যা আমাদের ডেটার বৈশিষ্ট্য বুঝতে সাহায্য করে।
সূচাঁলতা (Measures of Dispersion) পরিমাপ করার জন্য বিভিন্ন পদ্ধতি ও পরিসংখ্যানগত পন্থা ব্যবহার করা হয়। এটি তথ্যের ছড়িয়ে থাকার মাত্রা নির্ধারণে সাহায্য করে। সাধারণত সূচাঁলতা পরিমাপের মাধ্যমে বোঝা যায় যে, ডেটাসেটটি কতটা পরিবর্তনশীল বা কেন্দ্র থেকে কতটা বিচ্যুত। নিচে প্রধান সূচাঁলতা পরিমাপসমূহ আলোচনা করা হলো:
সূত্র:
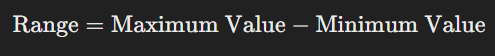

সূত্র:
যেখানে \( Q1 \) হলো প্রথম চতুরক এবং \( Q3 \) হলো তৃতীয় চতুরক।
সূত্র:

সূত্র:
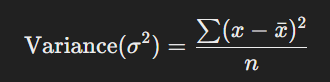
সূত্র:
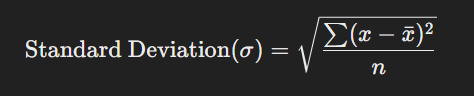
সূত্র:

সারসংক্ষেপ: সূচাঁলতা পরিমাপ ডেটাসেটের পরিবর্তনশীলতা এবং বৈচিত্র্য নির্ধারণে গুরুত্বপূর্ণ ভূমিকা পালন করে। বিভিন্ন পরিস্থিতিতে নির্দিষ্ট সূচাঁলতা পরিমাপ পদ্ধতি ব্যবহার করা হয়।
পাঁচ সংখ্যা সার হলো ডেটাসেটের সার্বিক বৈশিষ্ট্য বোঝানোর একটি পরিসংখ্যানিক পদ্ধতি। এটি ডেটাসেটের কেন্দ্রীয় প্রবণতা এবং বৈচিত্র্যের একটি ধারণা দেয়। পাঁচ সংখ্যা সার সাধারণত ডেটার পাঁচটি নির্দিষ্ট মান নিয়ে গঠিত:
১. সর্বনিম্ন মান (Minimum):
ডেটাসেটের মধ্যে সর্বনিম্ন মান।
২. প্রথম চতুর্ভাগ (Q1):
ডেটাসেটের প্রথম ২৫% মান পর্যন্ত অংশের মধ্যবর্তী মান। একে নিম্ন চতুর্ভাগও বলা হয়।
৩. মধ্যক (Median বা Q2):
ডেটাসেটের কেন্দ্রস্থলে অবস্থিত মান, যা ডেটাকে দুই ভাগে বিভক্ত করে।
৪. তৃতীয় চতুর্ভাগ (Q3):
ডেটাসেটের প্রথম ৭৫% মান পর্যন্ত অংশের মধ্যবর্তী মান। একে উপরের চতুর্ভাগও বলা হয়।
৫. সর্বোচ্চ মান (Maximum):
ডেটাসেটের মধ্যে সর্বোচ্চ মান।
ডেটাসেট: 5, 7, 8, 10, 12, 15, 18, 20, 25
পাঁচ সংখ্যা সার নির্ণয়:
১. সর্বনিম্ন মান:5
২. প্রথম চতুর্ভাগ Q1: 8
৩. মধ্যক (Median): 12
৪. তৃতীয় চতুর্ভাগ (Q3): 18
৫. সর্বোচ্চ মান: 25
পাঁচ সংখ্যা সার: 5, 8, 12, 18, 25
১. ডেটার বিস্তার নির্ধারণ:
সর্বনিম্ন এবং সর্বোচ্চ মানের মাধ্যমে ডেটার বিস্তার (Range) নির্ধারণ করা যায়।
২. বণ্টন বিশ্লেষণ:
চতুর্ভাগগুলো ডেটার বণ্টন এবং বৈচিত্র্য বিশ্লেষণে সহায়ক।
৩. আউটলাইয়ার শনাক্তকরণ:
চতুর্ভাগের মাধ্যমে বহিরাগত মান বা আউটলাইয়ার শনাক্ত করা যায়।
৪. চিত্রায়ণে ব্যবহার:
বক্সপ্লট তৈরিতে পাঁচ সংখ্যা সার ব্যবহার করা হয়, যা ডেটাসেটের ভিজ্যুয়াল বিশ্লেষণে সহায়ক।
পাঁচ সংখ্যা সার একটি সহজ এবং কার্যকর পদ্ধতি যা ডেটাসেটের কেন্দ্রীয় প্রবণতা এবং বৈচিত্র্যের সার্বিক ধারণা দেয়। এটি গবেষণা, সিদ্ধান্ত গ্রহণ এবং পরিসংখ্যানিক বিশ্লেষণে গুরুত্বপূর্ণ ভূমিকা পালন করে।
বক্স ও হুইস্কার প্রদর্শনী ডেটা বিশ্লেষণের একটি চিত্রভিত্তিক উপায় যা ডেটার বন্টন, কেন্দ্রীয় প্রবণতা এবং ছড়িয়ে পড়া সম্পর্কে ধারণা প্রদান করে। এটি একটি "পাঁচ-সংখ্যা সারসংক্ষেপ" (Five-Number Summary) ব্যবহার করে ডেটা উপস্থাপন করে।
বক্স ও হুইস্কার প্রদর্শনীতে প্রধানত নিচের উপাদানগুলো থাকে:
১. বক্স তৈরি করুন:
২. মধ্যমা চিহ্নিত করুন:
৩. হুইস্কার যোগ করুন:
৪. বহিরাগত মান (Outliers) চিহ্নিত করুন:

ধরা যাক, একটি ডেটা সেট:
2, 4, 5, 7, 8, 10, 12, 15, 18, 20
এগুলোর ভিত্তিতে বক্স ও হুইস্কার প্রদর্শনী তৈরি করা যায়।
বক্স ও হুইস্কার প্রদর্শনী একটি কার্যকর উপায় ডেটার বন্টন, ছড়িয়ে পড়া, এবং কেন্দ্রীয় প্রবণতা সম্পর্কে দ্রুত ধারণা পাওয়ার জন্য। এটি ডেটা বিশ্লেষণের ক্ষেত্রে একটি গুরুত্বপূর্ণ চিত্রভিত্তিক টুল।
বক্স এবং হুইস্কার প্লট (Box and Whisker Plot) একটি পরিসংখ্যানগত চিত্র, যা ডেটাসেটের কেন্দ্রীয় প্রবণতা এবং ছড়িয়ে থাকার মাত্রা সহজে বোঝার জন্য ব্যবহার করা হয়। এটি তথ্যের সারসংক্ষেপ প্রদান করে এবং তথ্যের বিভাজন ও বিচ্যুতির উপর আলোকপাত করে।
একটি পরীক্ষার নম্বর বিশ্লেষণের ক্ষেত্রে:
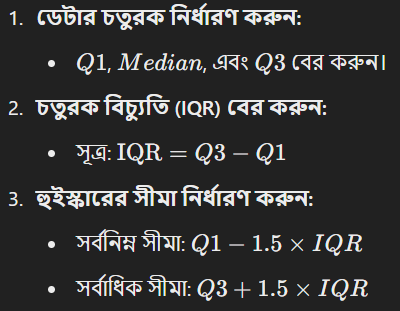
বক্স এবং হুইস্কার প্লট ডেটা বিশ্লেষণের একটি শক্তিশালী হাতিয়ার। এটি তথ্যের কেন্দ্রীয় প্রবণতা, ছড়িয়ে থাকা, এবং আউটলাইয়ার সহজে প্রদর্শন করে। সিদ্ধান্ত গ্রহণে এবং বিভিন্ন ডেটাসেটের তুলনায় এটি অত্যন্ত কার্যকর।
বক্স প্লট (Box Plot) একটি গ্রাফিক্যাল টুল, যা ডেটার বিস্তৃতি এবং বৈচিত্র্যকে সহজে বোঝার জন্য ব্যবহৃত হয়। এটি ডেটার বিভিন্ন পরিসংখ্যানিক গুণাবলী যেমন মিডিয়ান, কিউটাইল এবং আউটলায়ার সহজে চিহ্নিত করতে সাহায্য করে। নিচে বক্স প্লটের কিছু গুরুত্বপূর্ণ সুবিধা উল্লেখ করা হলো:
সারসংক্ষেপ: বক্স প্লট ডেটা বিশ্লেষণের একটি কার্যকর টুল যা ডেটার বিস্তৃতি, বৈচিত্র্য এবং আউটলায়ার চিহ্নিত করার পাশাপাশি তুলনামূলক বিশ্লেষণ সহজ করে। এটি বড় ডেটাসেটের ক্ষেত্রে অত্যন্ত সময়সাশ্রয়ী এবং কার্যকর।
Read more